6 математических задач, за решение которых можно получить $1 миллион

В 2010 году российский математик Григорий Перельман отказался от премии в размере $1 миллиона за решение одной из Задач Тысячелетия — гипотезы Пуанкаре. Но в мире остались ещё шесть математических проблем, за решение которых можно получить такую же внушительную сумму и международное признание. Разберёмся, почему каждая из этих задач уникальна и почему их решение может изменить мир.

Задачи тысячелетия

В 2000 году, вдохновившись знаменитым списком из 23 проблем Давида Гильберта, который определил развитие математики в XX веке, Институт математики Клэя (CMI) учредил «Премии тысячелетия». Научный совет института отобрал семь сложнейших задач из разных областей — от информатики до физики, — которые годами не поддавались решению.

За первое верное решение каждой из них CMI пообещал приз в $1 миллион. Однако цель этой инициативы — не просто раздать деньги. Это продолжение давней традиции, где сложные нерешённые задачи служат катализатором для инноваций. Сама попытка найти решение, даже неудачная, приводит к появлению новых теорий и открытий, подобно тому как космическая гонка породила множество побочных технологий.

Правила присуждения премии строги: решение должно быть опубликовано в авторитетном рецензируемом журнале и получить всеобщее признание в математическом сообществе в течение двух лет. Только после этого специальный комитет проверит работу.

За более чем 20 лет была решена лишь одна проблема — гипотеза Пуанкаре. Её доказал российский математик Григорий Перельман, который отказался от денежного приза из-за несогласия с позицией математического сообщества.

Оставшиеся шесть проблем так и остаются до конца не решёнными, хотя по каждой из них и есть определённый прогресс.

Равенство классов P и NP. Главный вопрос компьютерного мира

Эту проблему можно сформулировать одним вопросом: все ли задачи, чьё решение можно быстро проверить, можно так же быстро решить? «Быстро» в данном случае означает, что при увеличении объёма данных время на решение задачи растёт умеренно — не по степенному или экспоненциальному закону.

• Класс P — это задачи, которые можно быстро решить. Например, отсортировать список или найти самый короткий путь на карте.
• Класс NP — это задачи, где правильный ответ можно быстро проверить. Классический пример — игра судоку: решать её сложно, но если вам дадут готовое решение, вы легко проверите, верное ли оно.

Все задачи из класса P входят и в класс NP. Главный вопрос в том, равны ли эти два класса. Большинство учёных считают, что нет, но доказать это пока никто не смог.

Почему это важно

Разрешение этой проблемы изменит мир до неузнаваемости. Вот несколько областей, на которые оно повлияет:

• Криптография. Большинство современных систем шифрования, от банковских транзакций до криптовалют, основаны на предположении, что P не равно NP. Если окажется, что P=NP, любые шифры можно будет взломать, и вся существующая система кибербезопасности устареет в один момент.
• Оптимизация и наука. Многие сложнейшие задачи, такие как создание идеальных логистических маршрутов, разработка новых лекарств через моделирование белков, финансовое моделирование и даже автоматическое доказательство математических теорем, станут легко решаемыми.

Как сказал учёный Лэнс Фортноу, «то, что мы получим от P = NP, заставит весь интернет выглядеть как сноска в истории». Потенциальные выгоды для науки и экономики могут быть настолько огромными, что затмят проблемы с безопасностью.

Текущий статус

Проблема остаётся нерешённой. Главный аргумент в пользу того, что P≠NP, — это десятилетия безуспешных попыток найти быстрые алгоритмы для тысяч известных NP-задач. Попытки доказать это упёрлись в так называемые барьеры доказательств — существующие математические методы оказались недостаточными, а значит, для решения требуются совершенно новые подходы.

Гипотеза Римана. Тайна простых чисел

Это гипотеза о закономерностях в распределении простых чисел. Они кажутся разбросанными по числовой прямой без особого порядка. Но математики давно подозревают, что в этом «хаосе» есть скрытая закономерность.

Гипотеза Римана утверждает, что особая математическая функция, называемая дзета-функцией Римана, ведёт себя строго определённым образом: все точки, где она равна нулю, лежат на одной воображаемой линии. Это очень важно, потому что эти нули могут управлять тем, как распределяются простые числа.

Почему это важно

На распределении простых чисел построена вся современная криптография. Доказательство гипотезы даст полный контроль над этим распределением, что может как значительно усилить существующие системы шифрования, так и полностью их разрушить, сделав возможными новые, более эффективные атаки. В любом случае, разрешение гипотезы Римана заставит сферу кибербезопасности адаптироваться и развиваться, а не просто приведёт к её коллапсу.

© Wikimedia Commons

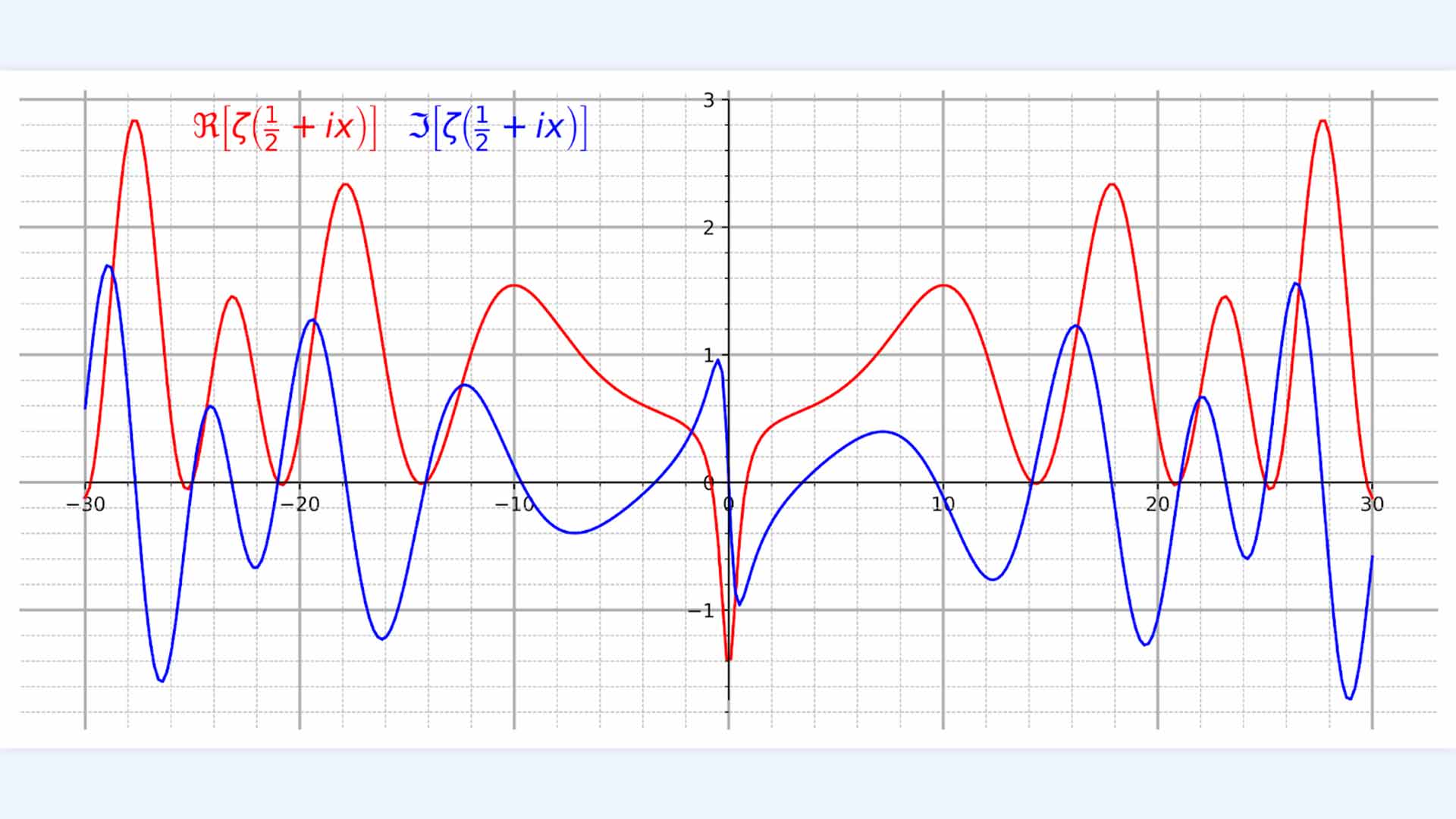
График двух компонент дзета-функции Римана — действительной и мнимой

Гипотеза Ходжа. Мост между мирами геометрии

Представьте себе разные формы в пространстве — например, бублик со сквозным отверстием или косточку от персика, где есть большое отверстие внутри и маленький канал между самой косточкой и её оболочкой. Математики, следуя идеям Ходжа, изучают такие «дыры» не просто как физические проходы, а через специальные математические объекты — дифференциальные формы и координатные функции. Этот подход помогает «заметить» и классифицировать все виды отверстий на сложных формах.

Учёные знают, что часть обнаруженных таким образом «абстрактных дыр» соответствует реальным подмножествам, заданным уравнениями. Но остаётся группа «дифференциальных» дыр, которым пока не удаётся найти геометрическую привязку. Гипотеза Ходжа утверждает, что каждый из этих особых типов дыр на самом деле можно описать как комбинацию других форм. Последние при этом имеют свои коэффициенты, описывающие вклад каждой подформы в общую форму. Интересно, что каждый из этих коэффициентов, согласно гипотезе, должен быть рациональным числом.

Это заявление проверено и доказано лишь в нескольких частных случаях, например, для некоторых поверхностей и низких размерностей, но в полном общепринятом виде остаётся нерешённой задачей.

Почему это важно

Это одна из фундаментальных проблем на стыке алгебры и геометрии. Её решение создаст новые мощные инструменты для изучения форм и пространств. Это важно для физики, в частности для теории струн, где геометрия сложных многомерных пространств играет ключевую роль. Решение гипотезы Ходжа может дать математическую основу для понимания фундаментальной структуры Вселенной.

Другие проблемы

Уравнения Навье-Стокса

Эти уравнения описывают движение жидкостей и газов. Они используются повсюду: от прогнозирования погоды и моделирования кровотока до создания реалистичных спецэффектов в кино. Однако математики до сих пор не знают, существуют ли для этих уравнений в трёхмерном пространстве всегда гладкие и однозначные решения, или они могут «сломаться», приведя, например, к бесконечной скорости потока. Доказательство этого стало бы первым шагом к математическому пониманию турбулентности.

© Wikimedia Commons

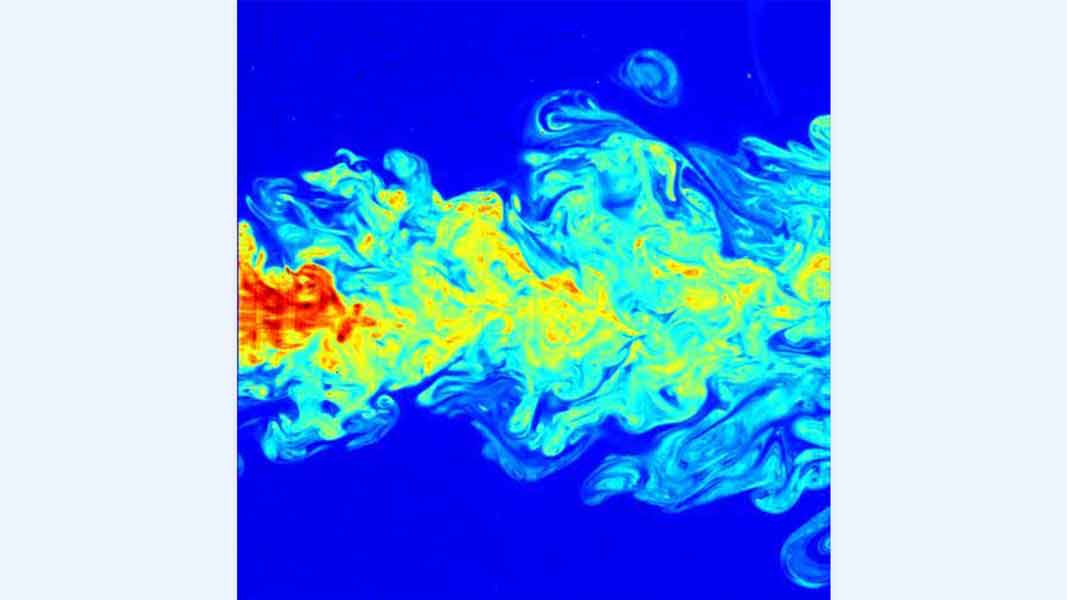
Визуализация турбулентного потока, описываемого уравнениями Навье-Стокса

Теория Янга-Миллса

Эта теория лежит в основе Стандартной модели физики элементарных частиц, которая описывает сильное и электрослабое взаимодействия. Проблема состоит в том, чтобы математически доказать, что эта теория корректна и имеет так называемую «щель масс». Это понятие объясняет, почему некоторые частицы, которые теоретически должны быть безмассовыми (например, глюоны), в реальности обретают массу, будучи «запертыми» внутри других частиц, таких как протоны и нейтроны. Решение этой задачи заполнило бы важнейший пробел в наших знаниях о фундаментальных силах Вселенной.

Гипотеза Бёрча и Суиннертон-Дайера

Эта гипотеза касается эллиптических кривых — объектов, задаваемых кубическими уравнениями. Она связывает количество рациональных решений (точек) на такой кривой с поведением связанной с ней математической функции (L-функции). Эллиптические кривые играют огромную роль в современной теории чисел и криптографии, и именно на них основывалось доказательство Великой теоремы Ферма. Решение этой гипотезы объединило бы несколько, казалось бы, разрозненных областей математики.

В итоге

Проблемы тысячелетия — это не просто изолированные головоломки, а фундаментальные вопросы, которые связывают разные области математики, физики и информатики. Их сложность заключается в том, что они затрагивают самые основы нашего понимания мира и требуют совершенно новых идей.

Стремление решить эти задачи, даже если оно не приводит к финальному ответу, стимулирует инновации и рождает новые теории. Путь к решению оказывается не менее ценным, чем само решение. Приз в миллион долларов — лишь мотивация для исследователей, а настоящая награда — это научный и технический прогресс, который даст решение каждой из этих задач.