Парадокс дней рождения: почему в комнате из 23 человек двое родились в один день
Эта ситуация кажется парадоксальной, но если собрать группу из 23 человек, то с вероятностью 50% у двоих из них день рождения будет в один день. А если в группе будет 57 человек, вероятность составит уже 99%. На первый взгляд кажется, что это какой-то абсурд, однако математика показывает обратное. Давайте разберёмся, почему наша интуиция так сильно ошибается и как этот забавный факт используется в технологиях.

В чём ошибка интуиции?
Главная проблема в том, что люди инстинктивно задают себе не тот вопрос. Они спрашивают «Какова вероятность, что кто-то в этой комнате родился в мой день рождения?». В этом случае вы сравниваете 22 других человека с одной-единственной датой. Вероятность такого совпадения действительно очень низка — для группы из 23 человек она составляет всего около 6%.
Но правильный вопрос такой: «Какова вероятность, что любые два человека в комнате родились в любой общий день?». Этот сдвиг в формулировке всё меняет, ведь теперь надо искать не совпадение с одной конкретной датой, а любое совпадение среди всех возможных пар людей.
Когда человек думает о своём дне рождения, то получает всего 22 сравнения. Но люди полностью упускают из виду огромное количество сравнений между всеми остальными людьми в комнате.
Секрет в парах, а не в людях
Секрет парадокса кроется в комбинаторике — подсчёте того, как быстро растёт количество пар. Количество уникальных пар для сравнения растёт гораздо быстрее, чем количество людей. Количество пар в группе из N человек рассчитывается по формуле Nx(N-1)/2. Посмотрите, как быстро оно растёт:
- В группе из 2 человек — всего 1 пара.
- В группе из 10 человек — уже 45 пар.
- В группе из 23 человек — 253 пары!
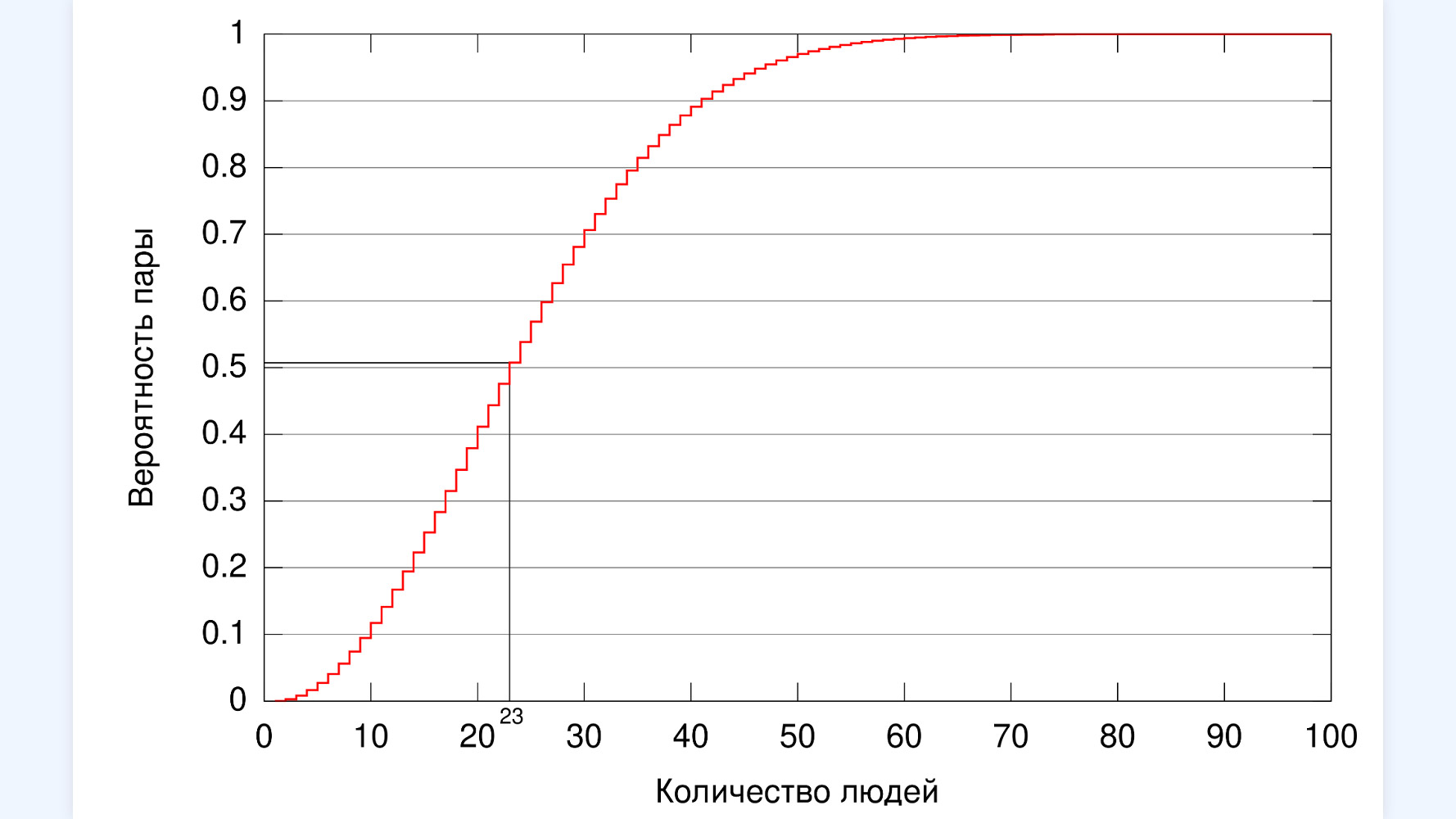
График зависимости вероятности совпадения дней рождения хотя бы у двух человек от количества людей
Таким образом, есть не 23 шанса на совпадение, а 253 шанса. Это огромное количество возможностей и является причиной того, почему вероятность совпадения так высока.
Как это посчитать?
Напрямую вычислить вероятность «хотя бы одного совпадения» очень сложно. Поэтому математики идут от обратного: они вычисляют вероятность того, что совпадений нет. То есть, что все 23 человека родились в разные дни. Логика такая:
- Берём первого человека. Он может родиться в любой из 365 дней. Шанс на уникальный день рождения — 100% (или 365/365).
- Берём второго. Чтобы его день рождения не совпал с первым, у него остаётся 364 дня из 365. Вероятность — 364/365.
- Берём третьего. Чтобы он не совпал с первыми двумя, у него остаётся 363 дня. Вероятность — 363/365.
- И так далее до 23-го человека.
Чтобы получить общую вероятность того, что все 23 человека родились в разные дни, нужно перемножить все эти вероятности. Результат этого умножения — примерно 49,3%. Это вероятность того, что все 23 человека родятся в разные дни. Соответственно, вероятность того, что есть хотя бы одно совпадение, — это всё остальное. И она равна 50,7%.
Как только количество людей превышает отметку в 23 человека, вероятность продолжает расти очень быстро. Например, для 41 человека она превышает 90%, а для 75 человек — 99,9%.
Атака «дней рождения»
Этот математический принцип — не просто забавный трюк. Он имеет решающее значение для кибербезопасности, особенно для хеш-функций.
Хеш-функция — это алгоритм, который берёт любые данные (пароль, файл, сообщение) и превращает их в короткий код фиксированной длины, называемый «хешем». Например, ваш пароль Password123 может превратиться в хеш e10adc3949ba59abbe56e057f20f883e. Надёжная хеш-функция должна быть устойчива к коллизиям — это ситуация, когда два разных входных файла, например, два разных пароля, вдруг дают одинаковый хеш. И здесь в игру вступает парадокс дней рождения.
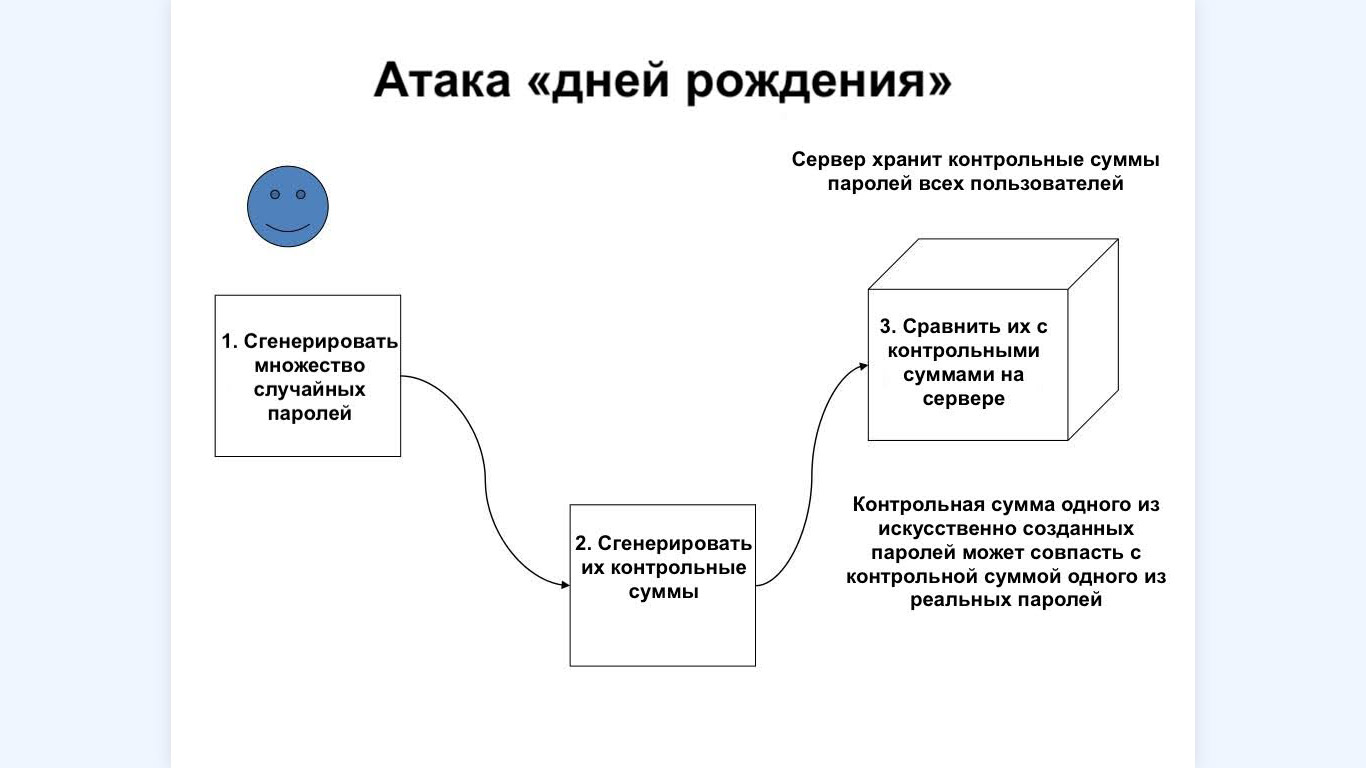
Схема атаки «дней рождения»
Атака «дней рождения» (Birthday Attack) — это метод поиска коллизий, который использует ту же логику: найти любые два разных сообщения, дающих один хеш, экспоненциально проще, чем подобрать сообщение под один конкретный хеш.
Представьте, что у хеш-функции N бит на выходе. Это даёт 2^N возможных вариантов хеша (это «дни в году» из примера с днями рождений).
- Сложная атака: Злоумышленник хочет подобрать данные под конкретный хеш. Ему потребуется в среднем 2^N попыток.
- «Атака дней рождения»: Злоумышленник ищет любую коллизию. Благодаря парадоксу, ему потребуется около 2^(N/2) попыток. Это колоссальное снижение сложности.
Именно поэтому старые хеш-функции, такие как MD5 (128 бит), считаются небезопасными. Интуитивно кажется, что 2^128 вариантов — это надёжно. Но «атака дней рождения» снижает эту безопасность до 2^64 операций. Это всё ещё огромное число возможных вариантов, но уже вычислительно достижимое для современных мощностей.
Чтобы противостоять этой угрозе, современные стандарты, такие как SHA-256, используют 256-битные хеши. Атака «дней рождения» на такой хеш потребует 2^128 операций. Это число настолько астрономическое, что считается невыполнимым в обозримом будущем.
В итоге
Парадокс дней рождения — яркий пример того, как наша интуиция, привыкшая к линейному росту, терпит неудачу при столкновении с экспоненциальной силой комбинаторики.
В технологиях этот принцип превращается из забавного факта в неумолимый закон безопасности. Согласно ему, для защиты от взлома наши криптографические системы должны обладать экспоненциальным запасом прочности. Только это позвлит противостоять нелинейной угрозе, которую выявил этот парадокс.